Les coordonnées polaires
On peut aussi situer la projection (a) du point dans le plan de référence par rapport à une origine O et un axe OX dans le plan horizontal de référence. La projection sera située sur une droite passant par l'origine dont on donne l'angle () par rapport à l'axe de référence OX et sa distance (l) par rapport à l'origine. [A(l,a)]. 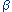Son éloignement par rapport au plan de référence sera donné par l'angle () que forme la droite passant par le point (A) et l'origine (O) avec sa projection dans le plan (Oa). [A(l,, )].

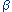Relation entre les coordonnées rectangulaires et les coordonnées polaires
Celles-ci sont établies à l'aide de la trigonométrie et du théorème de Pythagore
X / l = sin            y / l = cos           z / l = tg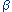

D'où :
X = l x sin           y = l x cos           z = l x tg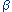
Inversement : L2 = x2 + y2 d'où l = racine (x2 + y 2) a = atan (y / x) ; b = atan (z / l)

[remarquer que plusieurs situations particulières ne sont pas déterminées et que pour interpréter correctement les angles on mettra l'origine de telle façon que l'objet à décrire soit contenu entièrement dans le cadran positif sur les 3 axes]