|
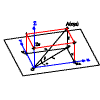
Fig. 3
|
On définira un point A dans l'espace par rapport à un plan de référence,
horizontal ou vertical. Le point est situé dans ce plan par sa projection
orthogonale sur celui-ci (a) [données de planimétrie] et son éloignement
au plan (A-a) [altimétrie pour un plan horizontal de référence].
Les coordonnées tri-rectangulaires
Pour décrire sa position dans l'espace, on utilisera un système de référence
de 3 axes orthonormés passant par une origine O. Les axes OX et OY définissent
le plan de référence horizontal, alors que l'axe OZ définit la normale
au plan c'est à dire la direction de projection sur celui-ci. La description
de sa position se fera, dans le plan horizontal, par les distances de
la projection (a) du point par rapport aux axes de référence OX et OY
[A(x,y)] alors que son éloignement par rapport au plan horizontal de
référence se mesurera sur l'axe OZ [A(x,y,z)]. Ce sont les coordonnées
d'un point. La valeur sur OX indiquera l'abscisse, la valeur sur Y l'ordonnée.[fig.3]
|