|
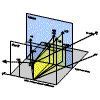
Fig. 2.2
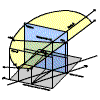
Fig. 2.3
|
Construction d'un point quelconque.
Chaque projection d'un point est le point de percé, sur le tableau,
d'une projetante issue de l'observateur et passant par ce point. Un
point M1, situé entre l'observateur O et le tableau aura son image en
m1. De même, un point M3 situé derrière le tableau aura son image en
m3. Un point M2 situé dans le tableau aura son image m2 confondue avec
le point lui-même. Un point M, situé à l'infini, aura son image en m,
représentation d'un point à l'infini. Un point M0 situé dans le plan
O' aura son image à l'infini sur le tableau, la projetante étant parallèle
à celui-ci.
Construction d'un droite quelconque.
Une droite D1 peut être vue comme un ensemble de points dont on doit
faire la projection par une projetante passant par O et le point à projeter.
L'ensemble des projetantes forment un plan projetant déterminé par la
droite D1 et l'observateur O, qui coupe le tableau en une droite, image
de la droite D1. Le point M0 de la droite, se projette à l'infini sur
le tableau. Le point M1, intersection de la droite et du tableau, sera
confondu avec son image. Le point à l'infini de la droite aura son image
en PfD1, intersection d'une projetante parallèle à la droite D1 avec
le tableau. Ce point est appelé "point de fuite de la droite" et représente
ses deux infinis. Chaque direction, dans l'espace, a un point de fuite.
On le trouve en faisant passer par l'observateur une parallèle à cette
direction et en trouvant son point de percé sur le tableau.
|